平衡二叉树
平衡二叉树英文叫Balanced Binary Tree,简称AVL,是为了解决二叉树搜索树极端情况下退化为线性结构的问题。
如何解决呢?
在插入或删除元素时,重新调整节点的排列顺序,使每个节点的左右两棵子树的高度相差不超过1
例如下图中,当插入新节点20时,红色节点28的左子树高度为2,右子树高度为0,那么这就不是一颗平衡二叉树
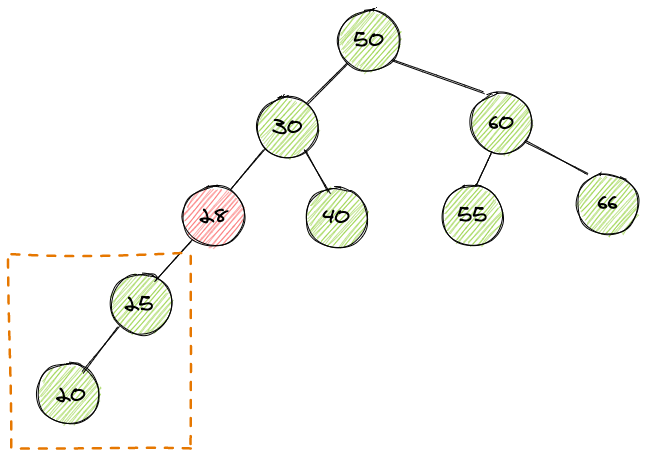
因此在插入新节点时,如果当前二叉树不平衡了,则需要调整节点的位置使其始终保持平衡
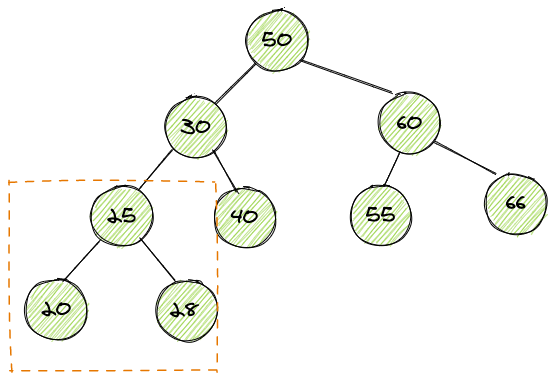
左旋
当插入一个新节点后,导致二叉树失衡,那么就需要通过旋转的方式使二叉树重新恢复平衡
当右子树比左子树高时,使用左旋,反之使用右旋
左旋的方法如下(假设要旋转的节点为A):
- A节点的右子节点替代A节点
- 右子节点的左子树变成A节点的右子树
- A节点变成右子节点的左子树
例如一个平衡二叉树插入了一个新节点:
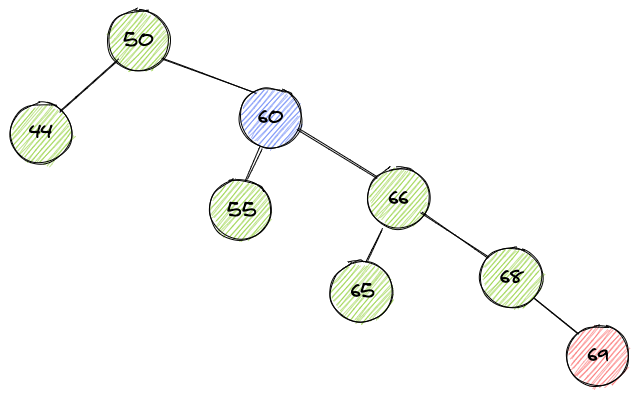
上图中,红色节点69为新插入的节点,导致二叉树失衡,紫色节点60的左子树高度为1,右子树高度为3,右比左高,需要左旋。
紫色节点60就是所谓的节点A,按照左旋的步骤依次执行:
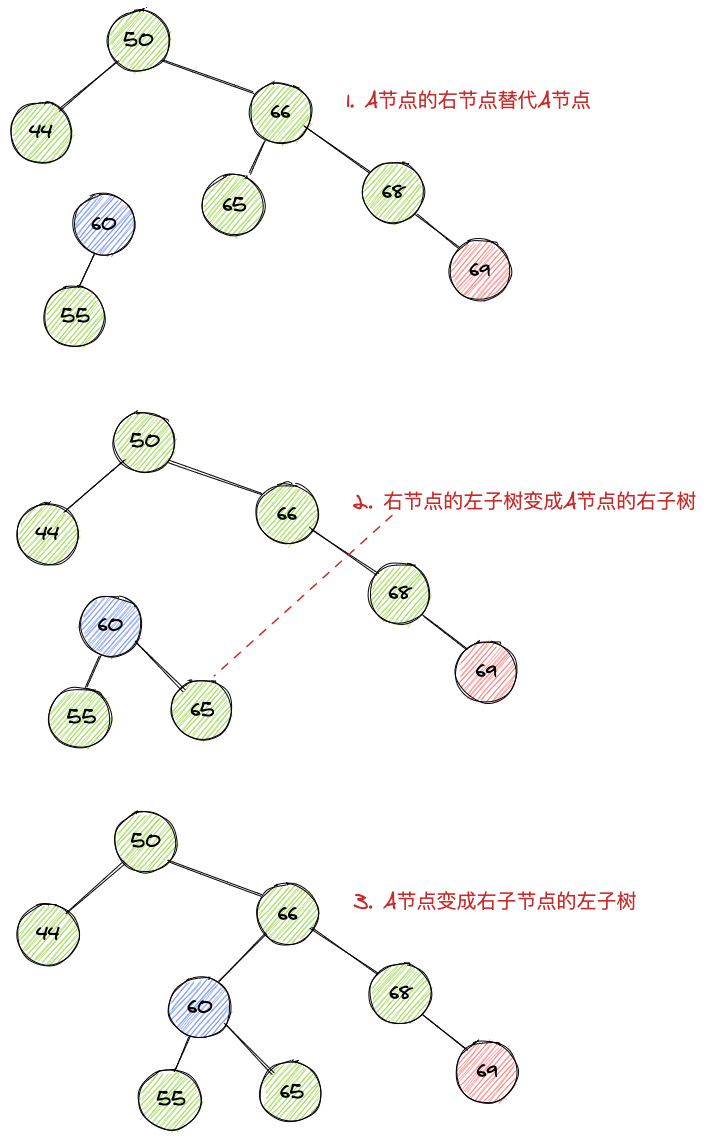
右旋
右旋的步骤其实和左旋一模一样,只不过把右变成左而已:
- A节点的左子节点替代A节点
- 左子节点的右子树变成A节点的左子树
- A节点变成左子节点的右子树
两次旋转
有一种特殊情况,进行了一次左旋或右旋之后,二叉树仍然不平衡,例如:
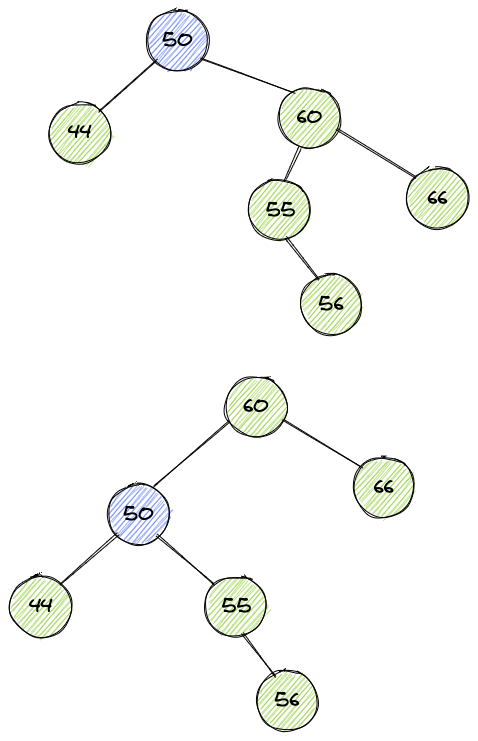
观察上图可以发现,紫色节点进行左旋之后,二叉树仍然不平衡,这种情况下应先对60节点进行旋转,得到如下图:
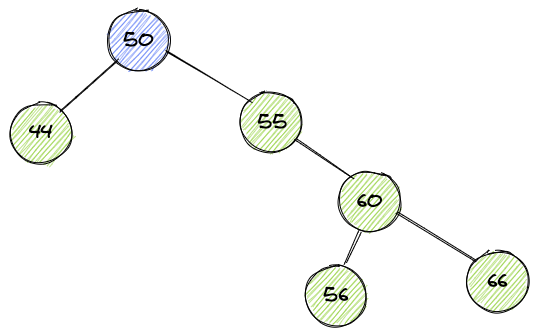
然后再给紫色节点做一次左旋即可

