跳表原理
在单向链表上,要查询一个数据,只能从头开始遍历,时间复杂度为O(n),那么有办法提高链表的查询速度吗?有,那就是跳表。
使用跳表有个前提,就是单链表本身是有序的
跳表的原理就是在原链表的基础上,每2个节点,创建一个索引,称之为一级索引,大致如下:
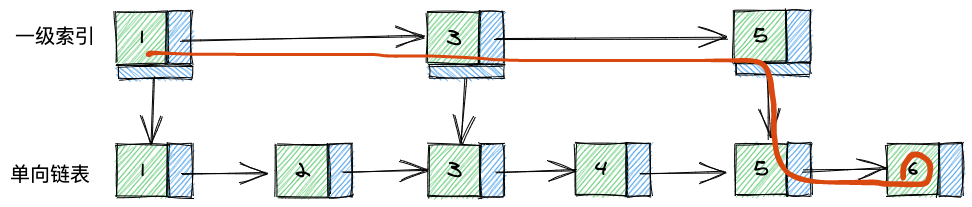
假设你要找6这个元素,原链表需要从1开始遍历,一共需要6次访问才能找到6,使用了跳表的一级索引之后,只需要1->3->5->6这个路径就找到了6。
在一级索引之上,我们可以再用同样的方法创建二级索引:
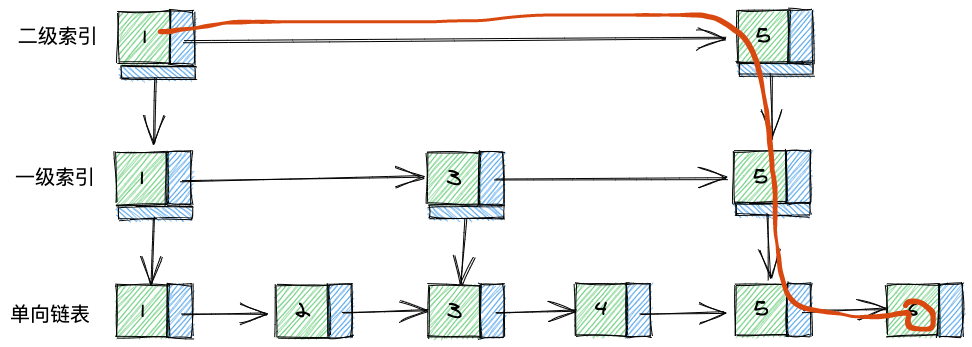
使用了二级索引,又减少了一次操作
当原链表数据量非常庞大时,我们可以创建多级索引。数据量越多,索引数越多,节省的时间也就越多。
可以看出,跳表是一个用空间换时间的数据结构
时间复杂度
假设单链表的长度为n,一共有k级索引,且最高级索引只有2个节点。
那么一级索引的的长度约为 $\frac {n} {2}$,二级索引长度就是$\frac {n} {4}$$,k级索引长度就是$$\frac {n} {2^k}$
因为最高级节点数为2,由$\frac {n} {2^k}$ = 2 可以得出索引数量k为
$$
\begin{align}
\frac {n} {2^k} &= 2 \\
n &= 2^{k+1} \\
k + 1 &= \log_2 n \\
k &= \log_2 n -1
\end{align}
$$
加上单链表,整个跳表的高度为$ h = \log_2 n $
如果每一层需要访问节点数为m,那么时间复杂度即为$O(m\log_2 n) $,平均时间复杂度可以省略倍数m,因此跳表的时间复杂度为$O(\log_2 n)$
空间复杂度
假设单链表长度为n,有k级索引,且最高级索引只有2个节点
一级索引的的长度约为 $\frac {n} {2}$,二级索引长度就是$\frac {n} {4}$$,k级索引长度就是$$\frac {n} {2^k}$
整个跳表的节点数为
$$
n + \frac {n} {2} + \frac {n} {4} + … + 2 = n(1 + \frac {1} {2} + \frac {1} {4} + … + 2)
$$
省略倍数,因此跳表空间复杂度为$O(n)$
如果觉得消耗内存太多,可以每3个节点生成一个索引,甚至每x个节点生成一个索引。
不过实际上不用太担心空间消耗问题,在实际开发中,原链表中的数据一般都是一个对象,而索引实际上只保存了对象的引用而已,不会占太多内存。
不仅如此,我们还可以将上图的跳表结构略作改造,不额外使用列表去保存索引,而是直接在原链表上做索引,又节省了不少空间:


